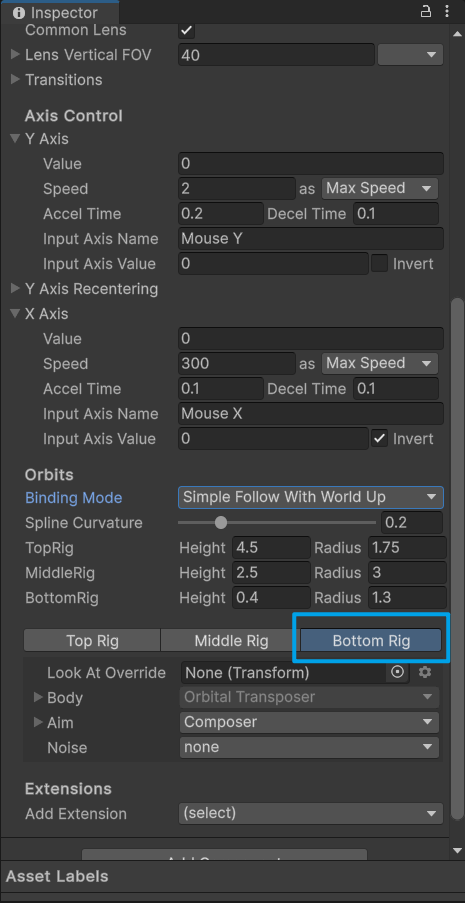
遍历二叉树
- 前序遍历NLR:先访问根结点,再前序遍历左子树,最后前序遍历右子树。
- 中序遍历LNR:先中序遍历左子树,再访问根结点,最后中序遍历右子树。
- 后序遍历 LRN:先后序遍历左子树,再后序遍历右子树,最后访问根结点。
- 层次遍历:自上而下、从左到右依次访问每层的结点。
前序遍历
144. 二叉树的前序遍历 - 力扣(LeetCode)
NLR
递归
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def preorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
res = [] # 用于存储遍历的结果
def helper(node):
# 如果当前节点为空,直接返回
if not node:
return
# 访问根节点
res.append(node.val)
# 递归遍历左子树
helper(node.left)
# 递归遍历右子树
helper(node.right)
# 从根节点开始递归遍历
helper(root)
return res
# 示例使用:
# 构建一个简单的二叉树
# 1
# / \
# 2 3
# / \
# 4 5
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
# 创建Solution对象并调用preorderTraversal方法
sol = Solution()
print(sol.preorderTraversal(root)) # 输出应为 [1, 2, 4, 5, 3]
后续遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
res = []
def helper(root):
if not root:
return
helper(root.left)
helper(root.right)
res.append(root.val)
helper(root)
return res中序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def inorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
res = []
def helper(root):
if not root:
return
helper(root.left)
res.append(root.val)
helper(root.right)
helper(root)
return res
层次遍历
是一种非常典型的广度优先搜索。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return []
res,cur_level = [],[root]
while cur_level:
temp = []
next_level = []
for i in cur_level:
temp.append(i.val)
if i.left:
next_level.append(i.left)
if i.right:
next_level.append(i.right)
res.append(temp)
cur_level = next_level
return res
重建二叉树
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
前序遍历的第一个元素为根节点,而在中序遍历中,该根节点所在位置的左侧为左子树,右侧为右子树。
我们可以根据中序数组的中间位置 1,来确定前序数组的左右部分,由于前序数组第一个是根节点,
所以其左边部分是:[1:mid_index],右半部分是 [mid_index+1:]

# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def buildTree(self, preorder, inorder):
"""
:type preorder: List[int]
:type inorder: List[int]
:rtype: TreeNode
"""
if len(inorder) == 0:
return None
# 前序遍历第一个值为根节点
root = TreeNode(preorder[0])
# 因为没有重复元素,所以可以直接根据值来查找根节点在中序遍历中的位置
mid = inorder.index(preorder[0])
# 构建左子树
root.left = self.buildTree(preorder[1:mid+1], inorder[:mid])
# 构建右子树
root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:])
return root
视图
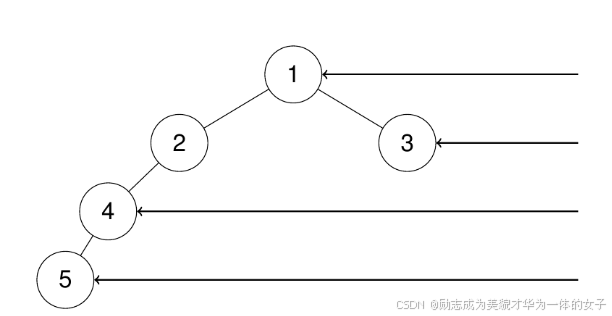
199. 二叉树的右视图 - 力扣(LeetCode)
树中根结点的层次为 0,其他结点的层次是父结点的层次加 1
树的深度是指树中所有结点的层次数的最大值加 1
递归
先递归右子树,再递归左子树,当某个深度首次到达时,对应的节点就在右视图中。
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
ans = []
def dfs(node: Optional[TreeNode], depth: int) -> None:
if node is None:
return
if depth == len(ans): # 这个深度首次遇到
ans.append(node.val)
dfs(node.right, depth + 1) # 先递归右子树,保证首次遇到的一定是最右边的节点
dfs(node.left, depth + 1)
dfs(root, 0)
return ans
时间复杂度:O(n),其中 n 是二叉树的节点个数。
空间复杂度:O(h),其中 h 是二叉树的高度。递归需要 O(h) 的栈空间。最坏情况下,二叉树退化成一条链,递归需要 O(n) 的栈空间。
二叉搜索树
二叉查找树(BinarySearch Tree)或者是一棵空树,或者是具有下列性质的二叉树:
1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2)若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3)任意节点的左、右子树也分别为二叉查找树。
二叉查找树性质:对二叉查找树进行中序遍历,即可得到有序的数列。
复杂度分析
它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。
构建二叉搜索树:依次插入就可以

如果删除的是只有左子树或者右子树的节点,先找到节点的位置,让这个子树替代这个节点然后删除这个子树的节点
如果删除的节点有左右子树,找到这个节点的左子树中最大的节点,代替这个节点,然后删除这个最大的节点,或者找右子树中最小的去替代这个节点去代替他。

108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode)
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
# 把 nums[left:right] 转成平衡二叉搜索树
def dfs(left: int, right: int) -> Optional[TreeNode]:
if left == right:
return None
m = (left + right) // 2
return TreeNode(nums[m], dfs(left, m), dfs(m + 1, right))
return dfs(0, len(nums))
109. 有序链表转换二叉搜索树 - 力扣(LeetCodF

class Solution:
def sortedListToBST(self, head: ListNode) -> TreeNode:
if not head:
return None
elif not head.next:
return TreeNode(head.val)
pre, slow, fast = None, head, head
while fast and fast.next:
pre = slow
slow = slow.next
fast = fast.next.next
root = TreeNode(slow.val)
pre.next = None
root.left = self.sortedListToBST(head)
root.right = self.sortedListToBST(slow.next)
return root
230. 二叉搜索树中第 K 小的元素 - 力扣(LeetCode)
二叉搜索树(BST)的中序遍历是有序的
# 定义二叉树节点的类
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
# 初始化节点,val是节点的值,left和right分别指向左子节点和右子节点
self.val = val
self.left = left
self.right = right
# 定义解决第k小元素问题的类
class Solution(object):
def kthSmallest(self, root, k):
# 初始化结果变量res和计数器k
self.res = None
self.k = k
# 调用深度优先搜索函数dfs
self.dfs(root)
# 返回找到的第k小的值
return self.res
def dfs(self, node):
# 如果节点为空或者计数器k已经为0,直接返回
if not node or self.k == 0:
return
# 递归地遍历左子树
self.dfs(node.left)
# 遍历完左子树后,计数器减1
self.k -= 1
# 如果计数器为0,说明找到了第k小的元素
if self.k == 0:
# 将当前节点的值赋给res
self.res = node.val
# 并返回,结束递归
return
# 如果计数器不为0,继续递归遍历右子树
self.dfs(node.right)
# 示例使用:
# 构建一个二叉搜索树
# 3
# / \
# 1 4
# \
# 2
root = TreeNode(3)
root.left = TreeNode(1)
root.right = TreeNode(4)
root.left.right = TreeNode(2)
# 实例化 Solution 类
sol = Solution()
# 调用 kthSmallest 方法寻找第1小的元素
print(sol.kthSmallest(root, 1)) # 输出应该是 1,因为第1小的元素是198. 验证二叉搜索树 - 力扣(LeetCode)
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def isValidBST(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
return self.helper(root, float('-inf'), float('inf'))
def helper(self, node, min_val, max_val):
# 如果节点为空,说明已经越过叶子节点,返回True
if not node:
return True
# 如果当前节点的值不在(min_val, max_val)范围内,则不是有效的BST
if not (min_val < node.val < max_val):
return False
# 递归检查左子树和右子树
# 左子树的最大值是当前节点的值,右子树的最小值是当前节点的值
return (self.helper(node.left, min_val, node.val) and
self.helper(node.right, node.val, max_val))
# 示例使用:
# 构建一个二叉树
# 2
# / \
# 1 3
root = TreeNode(2)
root.left = TreeNode(1)
root.right = TreeNode(3)
# 实例化 Solution 类并调用 isValidBST 方法
sol = Solution()
print(sol.isValidBST(root)) # 输出应该是 True,因为这是一个有效的BST求深度
104. 二叉树的最大深度 - 力扣(LeetCode)
树的遍历方式总体分为两类:深度优先搜索(DFS)、广度优先搜索(BFS)。
常见 DFS : 先序遍历、中序遍历、后序遍历。
常见 BFS : 层序遍历(即按层遍历)。
求树的深度需要遍历树的所有节点,基于 后序遍历(DFS) 和 层序遍历(BFS) 的两种解法。
后序遍历(DFS)
树的深度和其左(右)子树的深度之间的关系。显然,此树的深度 等于 左子树的深度 与 右子树的深度中的 最大值 +1 。
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root: return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
层序遍历(BFS)
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root: return 0
queue, res = [root], 0
while queue:
tmp = []
for node in queue:
if node.left: tmp.append(node.left)
if node.right: tmp.append(node.right)
queue = tmp
res += 1
return res
110. 平衡二叉树 - 力扣(LeetCode)
判断是否为平衡二叉树
平衡二叉树(AVL树)
1.使树在结构上左右分支平衡,所有节点的(左子树高度-右子树高度)的绝对值<=1。
2.平衡因子=左子树高度-右子树高度,所有节点的平衡因子的绝对值都小于等于1就是平衡二叉树。
3.也是二叉搜索树,只是操作后需要检查是否失衡,发现失衡后需要进行调整。
后序遍历+剪枝
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def recur(root):
if not root: return 0
left = recur(root.left)
if left == -1: return -1
right = recur(root.right)
if right == -1: return -1
return max(left, right) + 1 if abs(left - right) <= 1 else -1
return recur(root) != -1
求直径
543. 二叉树的直径 - 力扣(LeetCode)
- 对于树中的每个节点,计算其左子树和右子树的最大深度。
- 节点的直径可以通过左子树深度加上右子树深度再加1(当前节点)来计算。
- 更新一个全局变量,记录下所有节点直径的最大值。
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.val = value
self.left = left
self.right = right
class Solution:
def diameterOfBinaryTree(self, root):
self.max_diameter = 0
def depth(node):
if not node:
return 0
left_depth = depth(node.left)
right_depth = depth(node.right)
# 更新全局直径
self.max_diameter = max(self.max_diameter, left_depth + right_depth)
# 返回当前节点的深度
return max(left_depth, right_depth) + 1
depth(root)
return self.max_diameter
# 示例使用:
# 构建一个简单的二叉树
# 1
# / \
# 2 3
# / \
# 4 5
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
solution = Solution()
print(solution.diameterOfBinaryTree(root)) # 应该输出3,路径为4 -> 2 -> 1 -> 3对称
101. 对称二叉树 - 力扣(LeetCode)
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def isSymmetric(root):
def isMirror(t1, t2):
if not t1 and not t2:
return True
if not t1 or not t2:
return False
return (t1.val == t2.val) and isMirror(t1.right, t2.left) and isMirror(t1.left, t2.right)
return isMirror(root, root)
# 时间复杂度分析:
# 假设树有n个节点,那么每个节点都会被访问一次,所以时间复杂度是O(n)。
# 示例使用:
# 构建一个对称的二叉树
# 1
# / \
# 2 2
# / \ / \
# 3 4 4 3
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(2)
root.left.left = TreeNode(3)
root.left.right = TreeNode(4)
root.right.left = TreeNode(4)
root.right.right = TreeNode(3)
print(isSymmetric(root)) # 应该输出True,因为树是对称的- 时间复杂度:O(n),其中n是树中节点的数量。每个节点最多被访问两次,一次是在
isMirror函数的左边,一次是在右边。 - 空间复杂度:O(h),其中h是树的高度。这是由于递归调用的栈空间,最坏情况下树是线性的,空间复杂度为O(n),平均情况下是O(log n)。
翻转
226. 翻转二叉树 - 力扣(LeetCode)
BFS
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def invertTree(root):
if root is None:
return None
# 交换左右子树
root.left, root.right = root.right, root.left
# 递归反转左右子树
invertTree(root.left)
invertTree(root.right)
return root
# 时间复杂度分析:
# 假设树有n个节点,那么每个节点都会被访问一次,所以时间复杂度是O(n)。
# 空间复杂度分析:
# 空间复杂度是O(h),其中h是树的高度。这是由于递归调用的栈空间,
# 在最坏情况下(树完全倾斜),空间复杂度为O(n),在平均情况下(树比较平衡)为O(log n)。
# 示例使用:
# 构建一个简单的二叉树
# 1
# / \
# 2 3
# / \
# 4 5
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
# 反转二叉树
new_root = invertTree(root)最近公共祖先
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
DFS、递归

class TreeNode:
def __init__(self, x):
self.val = x # 节点的值
self.left = None # 左子节点
self.right = None # 右子节点
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
"""
在二叉树中找到节点p和节点q的最低公共祖先。
:param root: 二叉树的根节点
:param p: 二叉树中的第一个节点
:param q: 二叉树中的第二个节点
:return: 节点p和节点q的最低公共祖先
"""
def dfs(node):
# 如果当前节点为空,或者当前节点是p或q中的一个,直接返回当前节点
if not node or node == p or node == q:
return node
# 递归搜索左子树,寻找p或q
left = dfs(node.left)
# 递归搜索右子树,寻找p或q
right = dfs(node.right)
# 如果左子树和右子树都找到了p或q,说明当前节点是它们的最低公共祖先
if left and right:
return node
# 如果只有左子树找到了p或q,返回左子树的查找结果
# 否则返回右子树的查找结果
return left if left else right
# 从根节点开始深度优先搜索
return dfs(root)
# 使用示例:
# 构建二叉树
# 3
# / \
# 5 1
# / \ / \
# 6 2 0 8
# / \
# 7 4
root = TreeNode(3)
root.left = TreeNode(5)
root.right = TreeNode(1)
root.left.left = TreeNode(6)
root.left.right = TreeNode(2)
root.right.left = TreeNode(0)
root.right.right = TreeNode(8)
root.left.right.left = TreeNode(7)
root.left.right.right = TreeNode(4)
# 创建Solution对象
solution = Solution()
# 找到节点5和节点1的最低公共祖先
lca = solution.lowestCommonAncestor(root, root.left, root.right)
print(lca.val) # 应该输出3,因为节点3是节点5和节点1的最低公共祖先路径
112. 路径总和 - 力扣(LeetCode)
给定 二叉树 和 targetSum,如果树具有根到叶路径,则返回,使得沿路径的所有值相加等于 targetSum。
DFS:一直向下找到 叶子节点,如果到 叶子节点 时 sum == 0
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
if not root: return False
if not root.left and not root.right:
return sum == root.val
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
BFS 使用 队列 保存遍历到每个节点时的路径和,如果该节点恰好是叶子节点,并且 路径和 正好等于 sum,说明找到了解。
from collections import deque
from typing import Optional
# 定义二叉树节点的类
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def hasPathSum(self, root: Optional[TreeNode], sum: int) -> bool:
# 如果根节点为空,直接返回False
if not root:
return False
# 初始化队列,用于广度优先搜索
que = deque()
# 将根节点及其值加入队列
que.append((root, root.val))
# 开始广度优先搜索
while que:
# 从队列中取出节点和当前路径和
node, path = que.popleft()
# 检查当前节点是否为叶子节点且路径和等于目标和
if not node.left and not node.right and path == sum:
return True
# 如果有左子节点,将左子节点及其路径和加入队列
if node.left:
que.append((node.left, path + node.left.val))
# 如果有右子节点,将右子节点及其路径和加入队列
if node.right:
que.append((node.right, path + node.right.val))
# 如果遍历完所有节点都没有找到符合条件的路径,返回False
return False栈:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def hasPathSum(self, root, sum):
"""
:type root: TreeNode
:type sum: int
:rtype: bool
"""
if not root:
return False
stack = []
stack.append((root, root.val))
while stack:
node, path = stack.pop()
if not node.left and not node.right and path == sum:
return True
if node.left:
stack.append((node.left, path + node.left.val))
if node.right:
stack.append((node.right, path + node.right.val))
return False124. 二叉树中的最大路径和 - 力扣(LeetCode)
两个数的和:和自己父节点的和。3个数的和,和自己父节点的和再加上父节点的父节点或者兄弟的和。这样递归。这是一个深度优先搜索问题。一直到根节点结束计算。
lass TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def maxPathSum(self, root: TreeNode) -> int:
self.max_sum = float('-inf') # 初始化最大路径和为负无穷
def dfs(node, current_sum):
if not node:
return 0
# 当前路径和加上当前节点值
current_sum += node.val
# 更新全局最大路径和
self.max_sum = max(self.max_sum, current_sum)
# 递归计算左子树和右子树的最大路径和
left_sum = dfs(node.left, current_sum)
right_sum = dfs(node.right, current_sum)
# 返回当前节点的最大路径和,选择左子树或右子树中的较大者
return max(left_sum, right_sum)
# 从根节点开始递归
dfs(root, 0)
return self.max_sum
# 构建一个简单的二叉树进行测试
# 10
# / \
# 2 10
# / \ \
# 20 1 -25
# / \
# 3 4
root = TreeNode(10)
root.left = TreeNode(2, TreeNode(20), TreeNode(1))
root.right = TreeNode(10, None, TreeNode(-25, TreeNode(3), TreeNode(4)))
solution = Solution()
print(solution.maxPathSum(root)) # 应该输出 42 (20 + 2 + 10 + 10)深度优先搜索DFS
沿着一个分支遍历,直到这个分支的末端,然后回溯并探索另一个分支
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def dfs(node):
if node is None:
return
print(node.val) # 处理当前节点
dfs(node.left) # 递归遍历左子树
dfs(node.right) # 递归遍历右子树
# 使用示例
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
dfs(root) # 输出: 1 2 4 5 3200. 岛屿数量 - 力扣(LeetCode)
"岛屿"是指由水平或垂直相邻的1组成的区域,其中"相邻"意味着上下左右四个方向。

DFS
def num_islands_dfs(grid):
if not grid:
return 0
def dfs(grid, i, j):
# 检查边界条件和是否为水域
if i < 0 or i >= len(grid) or j < 0 or j >= len(grid[0]) or grid[i][j] != '1':
return
# 标记当前陆地为已访问(水域)
grid[i][j] = '0'
# 递归访问上下左右四个方向
dfs(grid, i-1, j)
dfs(grid, i+1, j)
dfs(grid, i, j-1)
dfs(grid, i, j+1)
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
# 如果遇到陆地,则进行深度优先搜索,并增加岛屿计数
if grid[i][j] == '1':
dfs(grid, i, j)
count += 1
return count
# 示例网格
grid = [
['1', '1', '0', '0', '0'],
['1', '1', '0', '0', '0'],
['0', '0', '1', '0', '0'],
['0', '0', '0', '1', '1']
]
print("Number of islands (DFS):", num_islands_dfs(grid))BFS
from collections import deque
def num_islands_bfs(grid):
if not grid:
return 0
def bfs(grid, i, j):
queue = deque([(i, j)])
while queue:
x, y = queue.popleft()
# 检查边界条件和是否为水域
if 0 <= x < len(grid) and 0 <= y < len(grid[0]) and grid[x][y] == '1':
# 标记当前陆地为已访问(水域)
grid[x][y] = '0'
# 将上下左右四个方向的陆地加入队列
queue.extend([(x-1, y), (x+1, y), (x, y-1), (x, y+1)])
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
# 如果遇到陆地,则进行广度优先搜索,并增加岛屿计数
if grid[i][j] == '1':
bfs(grid, i, j)
count += 1
return count
# 示例网格
grid = [
['1', '1', '0', '0', '0'],
['1', '1', '0', '0', '0'],
['0', '0', '1', '0', '0'],
['0', '0', '0', '1', '1']
]
print("Number of islands (BFS):", num_islands_bfs(grid))129. 求根节点到叶节点数字之和 - 力扣(LeetCode)

class Solution:
def sumNumbers(self, root: TreeNode) -> int:
if not root:
return 0
def dfs(node, num):
nonlocal res
if not node.left and not node.right:
res += num
return
if node.left:
dfs(node.left, num * 10 + node.left.val)
if node.right:
dfs(node.right, num * 10 + node.right.val)
res = 0
dfs(root, root.val)
return resBFS
class Solution:
def sumNumbers(self, root: TreeNode) -> int:
if not root:
return 0
queue = collections.deque([(root, root.val)])
res = 0
while queue:
node, num = queue.popleft()
if not node.left and not node.right:
res += num
if node.left:
queue.append((node.left, num * 10 + node.left.val))
if node.right:
queue.append((node.right, num * 10 + node.right.val))
return res
广度优先搜索BFS
按照层次顺序访问树或图的节点,首先访问最近的节点,然后逐渐向外扩展。
from collections import deque
def bfs(root):
if root is None:
return
queue = deque([root])
while queue:
node = queue.popleft() # 从队列中取出一个节点
print(node.val) # 处理当前节点
if node.left:
queue.append(node.left) # 将左子节点加入队列
if node.right:
queue.append(node.right) # 将右子节点加入队列
# 使用示例
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
bfs(root) # 输出: 1 2 3 4 5958. 二叉树的完全性检验 - 力扣(LeetCode)
在完全二叉树中,除了最后一个级之外,每个级都被完全填充,并且最后一个级别中的所有节点都尽可能靠左。
from collections import deque
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def isCompleteTree(root):
if not root:
return True
queue = deque([root])
end = False # 标记是否遇到一个节点没有右孩子
while queue:
node = queue.popleft()
# 如果遇到一个节点没有左孩子但有右孩子,返回False
if not node.left and node.right:
return False
# 如果遇到一个节点没有右孩子,标记end为True
if not node.right:
end = True
# 如果end为True,则后续的所有节点都必须是叶子节点
if end and (node.left or node.right):
return False
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return True
# 示例使用
# 构建一棵树进行测试
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
# 检验是否是完全二叉树
print(isCompleteTree(root)) # 应该输出True或False695. 岛屿的最大面积 - 力扣(LeetCode)
from collections import deque
def maxAreaOfIsland(grid):
if not grid:
return 0
rows, cols = len(grid), len(grid[0])
visited = [[False for _ in range(cols)] for _ in range(rows)]
max_area = 0
# 定义四个方向的移动
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
def bfs(r, c):
area = 1
queue = deque([(r, c)])
visited[r][c] = True
while queue:
x, y = queue.popleft()
for dx, dy in directions:
nx, ny = x + dx, y + dy
if 0 <= nx < rows and 0 <= ny < cols and not visited[nx][ny] and grid[nx][ny] == 1:
visited[nx][ny] = True
queue.append((nx, ny))
area += 1
return area
for i in range(rows):
for j in range(cols):
if grid[i][j] == 1 and not visited[i][j]:
max_area = max(max_area, bfs(i, j))
return max_area
# 示例使用
grid = [
[0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0],
[0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]
]
print(maxAreaOfIsland(grid)) # 输出应为最大的岛屿面积堆
根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆,堆总是一棵完全二叉树。
在优先队列中,元素按照优先级的高低排列,而不是按照它们进入队列的顺序。
215. 数组中的第K个最大元素 - 力扣(LeetCode)
堆排序
维护一个大小为k的最小堆,堆顶是这k个数里的最小的,遍历完数组后返回堆顶元素即可
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
heap = []
for num in nums:
heapq.heappush(heap, num)
if len(heap) > k:
heapq.heappop(heap)
return heap[0]